2.1.1 Tecnicas de conteo

Técnicas de conteo

A)    CONCEPTO.

Suponga que se encuentra al final de una línea de ensamble final de un producto y que un supervisor le ordena contar los elementos de un lote que se ha manufacturado hace unas horas y del que se desconoce el número de productos que lo constituyen, de inmediato usted empezará a contar un producto tras otro y al final informará al supervisor que son, 48, 54 u otro número cualquiera. Ahora suponga que ese mismo supervisor le plantea la siguiente pregunta ¿cuántas muestras o grupos será posible formar con los productos del lote, si las muestras o grupos a formar son de ocho elementos cada una de ellas?

En el primer caso el cuantificar los elementos del lote no presenta dificultad alguna para la persona encargada de hacerlo, pero cuando se le hace el segundo planteamiento, al tratar de formar las muestras o grupos de ocho elementos la persona encargada empezará a tener dificultad para hacerlo, en casos como este es necesario hacer uso de las técnicas de conteo para cuantificar los elementos del evento en cuestión (el número de muestras posibles a formar de ocho elementos), luego, ¿qué son las técnicas de conteo?

Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar.

Ejemplos en los que definitivamente haremos uso de las técnicas de conteo serían:

-¿Cuántas comisiones pro limpieza del instituto se pueden formar si hay 150 alumnos que desean ayudar en esta tarea y se desea formar comisiones de ocho alumnos?

-¿Cuántas representaciones de alumnos pueden ser formadas a) si se desea que estas consten solo de alumnos de Ingeniería Química?, b) se desea que el presidente sea un químico?, c) se desea que el presidente y tesorero sean químicos? Para todos los casos, se desea que las representaciones consten de once alumnos.

-¿Cuántas maneras tiene una persona de seleccionar una lavadora, una batidora y dos licuadoras, si encuentra en una tienda 8 modelos diferentes de lavadoras, 5 modelos diferentes de batidoras y 7 modelos diferentes de licuadoras?

Se les denomina técnicas de conteo a: las combinaciones, permutaciones y diagrama de árbol, las que a continuación se explicarán y hay que destacar que éstas nos proporcionan la información de  todas las maneras posibles en que ocurre un evento determinado.

Las bases para entender el uso de las técnicas de conteo son el principio multiplicativo y el aditivo, los que a continuación se definen y se hace uso de ellos.

Ejemplos

Aplicando el principio fundamental del conteo, tenemos 10 personas que pueden recibir el primer premio. Una vez que éste ha sido entregado, restan 9 personas para recibir el segundo, y posteriormente quedarán 8 personas para el tercer premio. De ahí que el número de maneras distintas de repartir los tres premios.

n

10 x 9 x 8 = 720

26 x 25 x 10 x 9 x 8 = 468000


Principio Aditivo y Multiplicativo

Principio Aditivo.

Dado que la probabilidad se refiere a la potencialidad de ocurrencia de un evento, el principio aditivo se refiere a las formas que ese evento puede ser realizado. Por ejemplo, una persona que define viajar desde Santiago al Litoral Central puede hacerlo por Línea de Buses A, Línea de Buses B, Línea de Buses C, Línea de Buses D. El principio aditivo, sería que cada línea de buses representa una alternativa:

L A= 1 ; L B = 1 ; L C = 1 ; L D = 1, (significa que cada línea de buses tiene una línea disponible al litoral central)

En el principio Aditivo sería, que la forma de llegar al punto L sería:

L = 1 + 1 + 1 + 1 = 4

La clave en el principio aditivo es buscar intrínsecamente la “0”, en el ejemplo, la persona para dirigirse al litoral central no puede utilizar todas las alternativas, tiene que utilizar una “o” la otra. Cuando se use el “o”, entonces hay que utilizar el principio aditivo.

Principio Multiplicativo.

El principio multiplicativo consiste en que, si existen distintas formas de que un evento suceda, y a su vez estas distintas formas tienen subformas de realizarse, se utiliza la multiplicación: se utiliza la cantidad de formas, por la cantidad de sub formas.

Por ejemplo, en el caso anterior, dado que existen cuatro líneas de buses, suponiendo que la línea A tenga cinco buses, la línea B tenga  cuatro buses, la línea C tenga dos buses y la línea D tenga ocho buses, entonces la forma de llegar a L, aplicando el principio multiplicativo, sería:

L = 1 x 5 + 1 x 4 + 1 x 2 + 1 x 8

Entonces el resultado sería   L = 19

Notacion factorial

Es el producto de los elementos positivos que van desde 1 hasta inclusive, se emplean con mucha frecuencia en matemáticas y se denota por el símbolo (n!) que se lee como "n factorial".

n! Tiene valores desde 1 hasta n.
n!=1...n.


Ejemplo:
          3!= 1.2.3=6
          2!=1.2=2
 
          5!=1.2.3.4.5=120


Encuentre el factorial de las siguientes cantidades.
a)      b!=720
b)       (4-2)!=2!=1*2=2
c)       (2+1)!=3!=6
d)      (3²)!=(9)!=362880
e)      (5-5+1)!=1!=1
f)       (2+1-3)!=0!=1
g)      8!=8.7.6!=8*7=56
h)      6!        6!

Propiedades de la notación factorial




 

REGLA DE LA SUMA

En la solución de algunos problemas es necesario considerar la probabilidad de que ocurra un suceso A o un suceso B (o de que ambos ocurran) como único resultado de un procedimiento. Esto se representa con la expresión P(A o B)

P(A o B) = P(Ocurre el suceso A u ocurre el suceso B o ambos)

- SUCESO COMPUESTO: Es cualquier suceso que combina dos o más sucesos simples.

- Para calcular la probabilidad de que un suceso A ocurra o un suceso B ocurra, se calcula el número total de formas en que A puede ocurrir y el número de formas en que B puede ocurrir, pero de tal forma que ningún resultado se cuente más de una vez.

EJEMPLOS:

1) Una máquina automática llena bolsas de plástico con una combinación de frijoles, brócoli y otras verduras. La mayoría de estas contiene el peso correcto, aunque, como consecuencia de a variación del tamaño de frijol y de algunas verduras, un paquete podría pesar menos o más. Una revisión de 4000 paquetes que se llenaron el mes previo arrojó los siguientes datos:

Peso	Evento	Número de paquetes
Menos peso	A	100
Peso satisfactorio	B	3600
Más peso	C	300

¿Cuál es la probabilidad de que un paquete en particular pese menos o más?

P(A o C) = P(A) + P(C)

              = (100/4000) + (300/4000)

              = 0.025 + 0.075

              = 0.1

Entonces lo multiplicamos por 100

0.1* 100 = 10%

Por lo tanto la probabilidad de que un paquete en particular pese menos o más, es del 10%

2)

200 turistas
120 de 200 van a Disneylandia

100 de 200 van a Busch Gardes

60 de 200 van a ambos lugares

P(Disney o Busch) = (120/200) + (100/200) + (60/200)

P(Disney o Busch) = 0.80

PERMUTACIONES

En matemáticas, dado un conjunto finito con todos sus elementos diferentes, llamamos permutación a cada una de las posibles ordenaciones de los elementos de dicho conjunto.

Cálcula las posibles agrupaciones que se pueden establecer con todos los elementos de un grupo, por lo tanto, lo que diferencia a cada subgrupo del resto es el orden de los elementos. Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para estos elementos: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1". 

EJEMPLOS:

1) ¿Cuántos números de 5 cifras diferentes se puede formar con los dígitos: 1, 2, 3, 4 y 5?

m = 5           y        n = 5

Si entran todos los elementos. De 5 dígitos entran sólo 3. Si importa el orden. Son números distintos el 123, 231, 321 No se repiten los elementos. El enunciado nos pide que las cifras sean diferentes.

Solución:

P5 = 5! = 5 * 4 * 3 * 2 * 2 = 120

2) ¿De cuántas maneras distintas pueden sentarse ocho personas en una fila de butacas?

Si entran todos los elementos. Tienen que sentarse las 8 personas.

Si importa el orden.

No se repiten los elementos. Una persona no se puede repetir.

Solución:

P8 = 8! = 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 40320

COMBINACIONES 

Una combinación, es un arreglo de elementos en donde no nos interesa el lugar o posición que ocupan los mismos dentro del arreglo. En una combinación nos interesa formar grupos y el contenido de los mismos.

Una combinación es un arreglo donde el orden NO es importante. La notación para las combinaciones es C(n,r) que es la cantidad de combinaciones de “n” elementos seleccionados, “r” a la vez. Es igual a la cantidad de permutaciones de “n” elementos tomados “r” a la vez dividido por “r” factorial. Esto sería P(n,r)/r! en notación matemática.

Permutaciones

Sí entran todos los elementos.

Sí importa el orden.

No se repiten los elementos.

Permutaciones circulares

Se utilizan cuando los elementos se han de ordenar "en círculo", (por ejemplo, los comensales en una mesa), de modo que el primer elemento que "se sitúe" en la muestra determina el principio y el final de muestra.

Permutaciones con repetición

Permutaciones con repetición de m elementos donde el primer elemento se repite a veces , el segundo b veces , el tercero c veces, ...(m = a + b + c + ... = n) son los distintos grupos que pueden formarse con esos m elementos de forma que :

Sí entran todos los elementos.

Sí importa el orden.

Sí se repiten los elementos.

Combinaciones

Se llama combinaciones de m elementos tomados de n en n (m ≥ n) a todas las agrupaciones posibles que pueden hacerse con los m elementos de forma que:

No entran todos los elementos.

No importa el orden.

No se repiten los elementos.

También podemos calcular las combinaciones mediante factoriales:

Combinaciones con repetición

Las combinaciones con repetición de m elementos tomados de n en n (m ≥ n), son los distintos grupos formados por n elementos de manera que:

No entran todos los elementos.

No importa el orden.

Sí se repiten los elementos.

Ejemplos Combinaciones y Permutaciones

EJEMPLOS:

1) En una clase de 35 alumnos se requiere elegir un comité formado por 3 alumnos. ¿Cuántos comités diferentes se pueden formar?

No entran todos los elementos.

No importa el orden.

No se repiten los elementos.

2) ¿De cuántas formas pueden mezclarse los siete colores del arcoíris tomándolos de 3 en 3?

No entran todos los elementos.

No importa el orden

No se repiten los elementos.

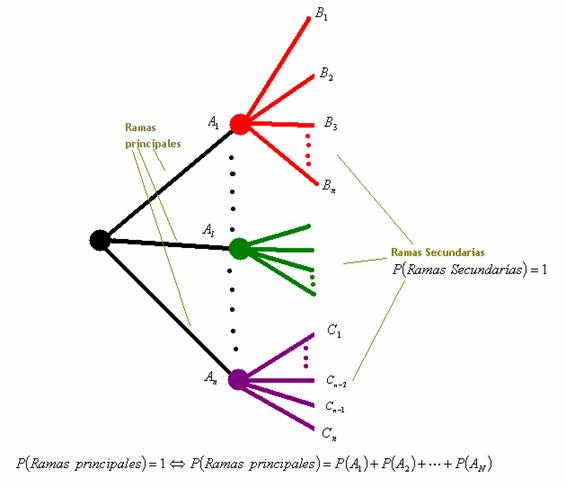
Diagrama de Árbol 

El diagrama de árbol es una representación gráfica de los posibles resultados del experimento, el cual consta de una serie de pasos, donde cada uno de estos tiene un número finito de maneras de ser llevado a cabo. Se utiliza en los problemas de conteo y probabilidad.

Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad.

En el final de cada rama parcial se constituye a su vez, un nudo del cual parten nuevas ramas, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final).

Hay que tener en cuenta: que la suma de probabilidades de las ramas de cada nudo ha de dar 1.

EJEMPLOS

Referencias:

itchihuahua. (2015). PROBABILIDAD Y ESTADÍSTICA. 2015, de itchihuahua Sitio web: http://www.itchihuahua.edu.mx/academic/industrial/sabaticorita/_private/01Concepto.html

UNAM. (2014). Tecnicas de conteo. 2014, de UNAM Sitio web: http://www.dcb.unam.mx/users/gustavorb/Probabilidad/PE13.pdf 

Escolares. (Desconocido). Escolares. Desconocido, de Escolares Sitio web: http://www.escolares.net/matematicas/probabilidades-principio-aditivo-y-multiplicativo/

Bligo. (2013). Probabilidad y Estadistica. 2013, de Bligo Sitio web: http://hortenciacecyt14.bligoo.com/probabilidad-y-estadistica#.WMRLtTmb_IU
 

Disfrutalasmatematicas. (2008). combinaciones y permutaciones. 2008, de disfrutalasmatematicas Sitio web: http://www.disfrutalasmatematicas.com/combinatoria/combinaciones-permutaciones.html

Rudy Gonzales (2012) Estadistica http://rudy-gonzalez.blogspot.mx/2010/09/combinaciones-y-permutaciones.html

 vi-tutor. (2012). Diagramas de arbol. 2012, de vi-tutor Sitio web: http://www.vitutor.com/pro/2/a_15.html

Enriquez Araiza, R. (23 de Febrero de 2014). Combinación, permutación, principio aditivo y principio multiplicativo. Obtenido de SlideShare.net: https://es.slideshare.net/RozytaBob/combinacin-permutacin-principio-aditivo-y-principio-multiplicativo